sprezzatech blog #0015
New Directions in Window Management, Part II.
Fri, 15 Mar 2013 04:41:39 -0400

NASA footage of Charn.
“It is silent now. But I have stood here when the whole air was full of the noises of Charn; the trampling of feet, the creaking of wheels, the cracking of the whips and the groaning of slaves, the thunder of chariots, and the sacrificial drums beating in the temples. I have stood here (but that was near the end) when the roar of battle went up from every street and the river of Charn ran red. And in one moment one woman blotted it out for ever.”
—C. S. Lewis, The Magician's Nephew (1955)
Diuinior et excellentior sit Triangulorum sphæricorum cognitio, quam fas sit eius mysteria omnibus propalare.
(The understanding of spherical triangles is so divine and elevated that extension of their understanding to everyone would be a sin.)
—Tycho Brahe, De Nova Stella (The New Star) (1593)
DISCLAIMER: I don't really know what I'm talking about below.
This is more true for this article than normal. There's possibly quite a bit
wrong. Most of this is based on intuition, and not rigorous proof or even
serious investigation. I am neither a trained geometer nor a competent
topologist. Should you have a 2-sphere you need inverted, consult your local
low-dimension rubbersheeters. They'll be glad to get the work.
Having discussed in Part I of this series the “WIMP paradigm” and trends in user interaction hardware, let's move on to the motivations and design of Charn. First, the basics:
- We aim for ICCCM 2.0 and EWMH 1.3/1.4draft2 compliance.
- We will employ OpenGL 3.1, as currently implemented by Mesa, and more advanced OpenGL ARBs as need be.
- We will target the X11R6 (X Windows Version 11 Release 6) backend, while designing for later support of Wayland, DirectFB, and/or the Linux framebuffer. “Mir”, should it actually emerge (I've got major doubts on Canonical's ability to deliver, and I say Canonical because Mir is 100% a Canonical thing, rather than a Ubuntu thing), can get fucked.
- It ought be possible to fully drive the system using any combination of any one or more input devices.
- Multihead, Zaphod mode, XRandR 1.4, all of that good stuff.
- Make full use of GPU capabilities, including where necessary using compute mode (CUDA/OpenCL) to process data so that trips across the system bus are minimized.
These seem to me fundamental requirements for any graphics system in Anno Domini 2013, i.e., if there's problems connecting to a projector, they had by god better be kernel or display server problems. Now, the more interesting stuff. Let's state some requirements, and see where they lead us. Now, by the way, might be a good time to read the 2004 report of Project Looking Glass. Of particular importance is consideration of both two- and three-dimensional applications within a three-dimensional system (consider, for instance, the dramatic possible differences between two- and three-dimensional applications' virtual traversal of a Möbius strip topology).
- Provide a geometric/topological model that allows coherent, intuitive manipulation of both two- and three-dimensional applications.
- While Charn supports discrete virtual desktops/workspaces, this ought only be a degenerate case of its continuous desktop.
- Charn ought provide a meaningful degree of freedom for every degree of freedom of feasible input devices. At the same time, devices with fewer degrees of freedom must still be able to drive Charn in its entirety.
- 2D windows must not be distorted, so long as they are no larger
than the viewport, when being used. This is trivially satisfied with a
two-dimensional topology, but in other numbers of dimensions, we must
ensure a conformal mapping up through a rectangle having the
dimensions of the viewport.
- Charn will implement a Zooming User Interface (ZUI). At the point of maximal antizoom, all applications ought be displayed on a single viewport.
- Support the interfaces necessary for efficient tiled window management, and tile by default through a viewport.
- Facilitate maximal utilization of display whenever and to whatever degree possible.
- Support maximal degrees of freedom when moving focus or view. Rather than absolute moves (characteristic of discrete workspaces), encourage moves relative to empty space or other windows along some vector.
- Support strewing operations (my nomenclature; if these have existed elsewhere, please let me know): hurl a window or group thereof along some vector to make space. There are two types of strewings: strewments and inflations. The former sends windows along a vector, coming to rest in empty space, possibly moving other windows along the way. If there is insufficient space to minimally preserve angles, the space instead ought be inflated. An inflation prefers to inflate immediately. The space ought automatically deflate when reasonable.
- It ought not be possible to reflect inputs by any rigid translations. Furthermore, it would be nice if windows never appear rotated, despite rotations of the surface itself.
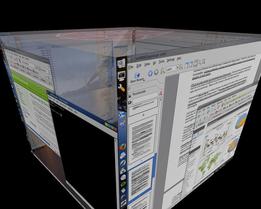
What do these requirements suggest? Keep in mind that all we have to work with in terms of display is a finite 2d rectilinear plane. No matter what model we might choose, in the end it must be meaningfully reduced to this rectangle. At first appearance, it might seem that the geometry of the cube is tailored to the problem, and indeed the Compiz window manager used by default in SprezzOS embraces a pseudo-generalization of the cube. So far as I know, this can be considered the state-of-the-art in open source 3D window management:
The cube is, of course, the 3-dimensional extension of a square (aka a 2-cube). This concept can be generalized to yield the 4-dimensional hypercube and subsequent n-cubes. The unit n-cube has an n-dimensional volume of 1 in any n dimensions.
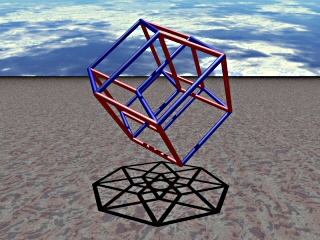
2- and 3-dimensional shadows of a 4-dimensional hypercube.

Hypercube rotating through a plane of projection.
Note that while Compiz also advertises “cylindrical” and “spherical” modes, there are purely visual deformations, applied only during cube rotation. At no point
Nota bene: Overlapping terminology henceforth is used primarily in its
cartographic sense, not mathematic. This is particularly troublesome
for "orthographic", which is a perspective projection in cartography
and a parallel projection in mathematics. I'll try to make it clear in
each context. If it makes you feel better, when you read something and
are confused, just assume I don't know what I'm talking about, because
you're probably right.
does a Compiz user manipulate window contents within a true spherical or cylindrical geometry;
terminating rotation results in a spontaneous symmetry break, snapping to
a face based on the current normal vector). Note that
already issues arise from the necessity of two-dimensional display: when viewing
the cube along a vector normal to some face, we can see only that face (a maximum
of 1/6 of the total surface area). The projective view utilized during rotations
makes visible 3 faces; the projection equalizing distortion among the 3 visible
faces yields a regular projective polyhedron known as the hemicube,
and results from tessellation of the real projective plane by three
quadrilaterals. Cartographers know these views as the tilted and
vertical general perspective projections; viewed from a point infinitely
distant, the vertical GPP gives rise to the (cartographic, see n.b. above)
orthographic projection; the finite and infinite versions comprise
the class of orthonormal projections. There are costs associated with
this greater visibility: neither original areas nor shapes have not been
preserved (distortion increases with distance from the viewer), and we no
longer fully utilize our display (obviously, showing more virtual area requires
scaling (zooming), but the ratio of real area to the product of virtual
area and scale decreases with increasing visible surface area). In general, I'm
fairly certain that an orthonormal projection cannot reveal more than 1/2 the
surface area of a solid exhibiting full rotational symmetry (read: unaware of a
proof, did not attempt to generate one, won't be shocked if proven wrong). On
the plus side, the projection keeps points which are close to one another on
the cube close to one another on the display—the volume has not been
torn or crumpled.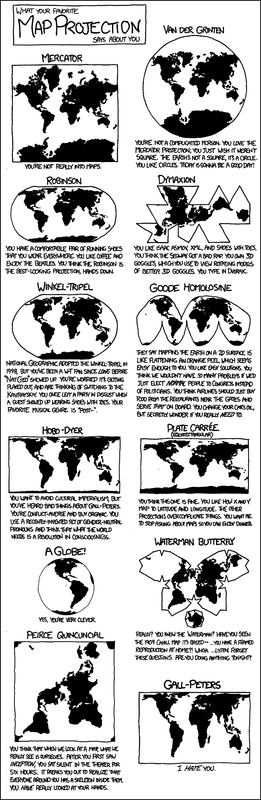
XKCD on projections (original).
Looking back at our criteria above, perhaps the most important is the requirement that naturally rectilinear windows not be distorted when viewed head-on. Without this requirement, we break invariants critical to the design of all existing software. What are these assumptions? Let's list some:
- Windows are rectilinear. Stated another way, “within the (implicitly quantized) area to which I can draw, every row has the same number of columns, and there are no further dimensions.”
- The user might resize (independently of rescaling) the window, but only in a rectilinear fashion.
- Physical and virtual displays' aspect ratios are constant.
- Different rows, and likewise different columns, do not intersect one another.
I numbered these purposefully—they ought immediately suggest the five axioms of Euclid's Elements (our #2 roughly corresponds to Euclid's #2 and #3). This is great! It means that these assumptions are equivalent to providing a two-dimensional Euclidean (virtual) geometry, a mathematical space (𝔼²) that's very well understood. Furthermore, it's a very good approximation of our universe's physical space (Aristotelian spacetime is 𝓐, the product space 𝔼³×𝔼; Galilean-Newtonian dynamics are a fibre bundle 𝓖 with base space 𝔼 and fibre 𝔼³, with Galilean transforms between reference frames; special relativity is a Minkowski spacetime 𝕄 (three spacelike and one timelike dimensions (pseudometric tensor signature +++- or +---)) hyperbolically rotated by the Lorentz transforms; general relativity (Einsteinian spacetime 𝓔) sees the stress-energy tensor curve the 4-manifold, subject to the requirement that tangent spaces are all Minkowski spaces. Interested readers are strongly advised to consult Penrose's The Road to Reality or Carroll's Spacetime and Geometry), and is thus as comfortable a space within which to work as humans are going to find. Let's thus establish a single hard requirement.
Thou shalt provide at least a local (finite) affine rectilinear Euclidean viewport (𝔼²) onto which windows can be mapped.
This would seem to restrict us pretty sharply in terms of underlying spaces! At first sight, we're restricted to either an infinite plane or a set of finite planes (we will henceforth assume all such arrangements to be convex hulls, without—I think—real loss of generality) and some arbitrary transition function between them (Compiz's “cube” is laid bare as a set of finite planes, each of which is assigned a map from 4-directional navigation to up to 4 different planes. The difference is in the rotational symmetry, which is different when transforming and working upon the Compiz volume). This kind of sucks, because no combination of planes meets many criteria from our original list. An infinite plane is not a compact space. Imagine a user who creates a window, moves to the right, creates a window, moves to the right, ad nauseam. Moving from window to window will either be “slow” (more operations to move from source to dest) or maximally arbitrary (i.e., with the least correspondence to visible navigation cues). It is worth noting that this property seems to be maintained across all factors of zoom and all possible space-filling curves. A set of finite planes, meanwhile, exhibits boundaries (at least as many boundaries as planes, and typically more), and suffers variation in symmetry as planes are added and removed, even among regular polyhedra.
Let topology ride to our rescue! An n-manifold is a topological space such that each point has a neighborhood resembling n-dimensional Euclidean space. A topological surface (henceforth just surface) is a two-dimensional manifold—more precisely, a “second countable Hausdorff topological space in which every point has an open neighborhood homeomorphic to some open subset of the Euclidean plane 𝔼²”. What does this mean for us? It means that, so long as the space is of scale, we can map windows to that fucker. This furthermore implies that, since we don't know that scale is needed in advance (it's a function of our viewport; see Dank's First Commandment), any space that works will allow us to map arbitrarily many windows, by inflating it dynamically. Fuck yeah, science!
So, what surfaces optimize for our original criteria?

Rectilinear mapping: The surfaces which can be unfolded to a rectangle without tearing or distortion are the developable surfaces. By Gauss's Theorema Egregium, we can show that these are precisely those surfaces having Gaussian curvature of 0. These include the plane, the (possibly truncated) cone, the cylinder, the torus, and the oloid. The Mercator (conformal) projection of Earth, for instance, projects Earth onto the inside of a cylinder tangent at the Equator, then flattens that cylinder.
Continuous desktop: A solid for which symmetry doesn't break when we move from our projective view (zoomed translations along the global surface) to our local Euclidean view is required to have no boundaries. If we restrict ourselves to boundaryless compact (closed) surfaces, the classification theorem thereof tells us that we need consider only:
- The 2-sphere
- The connected union of toruses
- The connected union of real projective planes
Symmetry: Symmetry in three dimensions is maximized by the 2-sphere (hence “spherical symmetry”. Toruses and open toruses, annuli, cylinders, and (possibly truncated) cones have axial symmetry. Regular polyhedra have the largest symmetry groups among polyhedrons.
Maximal use of display: I haven't worked this out yet. It's perhaps worth noting that a sphere mimimizes surface area for a given volume, while a tetrahedron maximizes surface area for a given volume enclosed within a regular polyhedron.
Alright, I have been working on this for about six hours now, and really want to do something else. To make a long story short, I'm pretty sure I want to model a sphere, though possibly a Klein bottle (the union of two real projective planes, a closed surface admitting no orientation and having no volume) or a torus, or a projective plane. More thought is needed, but I'm going to get some code down on paper and start manipulating things to get a more intuitive feel for them.
Hack on!