Check out my first novel, midnight's simulacra!
The Power, pt 1

hey there, my hax0rs and hax0rettes! it's been a good long time since we last got together, but i hope to make up for paucity and exiguity with a surfeit of ass-rocking quality. i rebuilt my workstation recently, and it left me with a few questions. i looked into the answers, and thought the investigation a good time, and maybe you'll likewise find it informative, entertaining, and even useful.
as always, we're gonna cover a lot of ground in an hour, all the way from a wall outlet, to the big bang, to refrigerator design, to the dance of electrons. i am *not* an expert on all of these topics, so definitely listen with a critical ear and watch with a scrupulous eye, but, you know, you really ought be doing that all the time. if i have a general theme tonight, i suppose that theme is: power.
in the world of huey lewis and the news, love can be measured in watts, the SI unit of power. love applied over time would furthermore be work, and measured in joules. but i'm an engineer, so this evening we'll be quantifying the power of love, but mainly the love electrons feel towards cations. this is DANKTECH!
Intro
so first i'd like to tell a little story from 2018. i had just started putting together a new machine. big plans, big dreams. i installed the psu, mated the cpu, and hung the mobo. now here i typically spin up this computational core of a new build. otherwise, if there's any problem, the first thing i'll be doing is stripping the box back down to these essentials. so i turn it on, and nothing. dead air. horror vacui. sigh. alright, let's first validate this power supply. now i've got an ATX power supply tester. you can pick one of these up for about fifteen bucks, and they're well worth it if you're fucking at all regularly with boxen.
[ demonstrate testing with PSU tester ]
actually, let's talk about ATX for just a second. ATX, "Advanced Technology eXtended", was a 1995 Intel standard for PSUs, motherboards, and chassis (chassis is borrowed from the french châsse, derived from the Latin capsa, meaning case or box, so calling your machine a box isn't just technohipster argot drivel). your rear I/O panel today has all kinds of crap undreamable in 1995, but it's still 158.75mm by 44.45mm because of a Clinton-era spec. The Advanced Technology being eXtended was that of the IBM 5170, the AT, introduced in 1984 and built around the 16-bit 286. It itself followed 1983's 5160 XT, a disappointing successor to the original 5150 IBM PC and its 4.77MHz 8088. If you're rummaging around at the dump looking for mechanical keyboard gold, and you find one of these ungainly 5-pin DIN connectors, that's from the XT.

And you're looking at an old keyboard indeed in that case, probably an IBM Model F. The famous Model M wasn't released until 1986, and the vast majority of them used the 6-pin PS/2 connector introduced in 1987. oh, man, and I could talk your heads off about keyboard technology, but it's a pretty niche area of interest, and our days are sadly numbered. It's kinda weird that ATX references the AT in its name, actually, since most of what it eXtended came from the PS/2, and you'll sometimes even come across the term "ATX/PS2 power supply". none of these IBM designs were really standards, though; they were just products, with which other vendors more or less interoperated, and often cloned. in fact, if you remember the ISA bus—the "Industry Standard Architecture" that preceded the VESA Local Bus and PCI—was just a renaming of the 8-bit XT and 16-bit AT IBM buses, in response to the proprietary MicroChannel Architecture bus introduced on the PS/2. by the way, you still have some AT naming legacy in your machine today—SATA is the serial version of the ATA, the AT Attachment, the AT's hookup to its 10 megabyte hard disk. and ATAPI is just a packet interface atop that. so raise a glass to William Lowe and Don Estridge and the IBM Boca Raton team; besieged by Compaq and Dell and Hewlett Packard, IBM lost the war, but their legacy lives on.
ATX is still the most common motherboard design for workstations, and other designs—mini-ATX, XL-ATX, SFX, etc.—are usually compatible with ATX in their common areas. so you almost certainly have the 24-pin power connector known as ATX12V.
ATX originally included three cables total:
- 4-pin 18 AWG AMP 1-480424-0 / Molex 15-24-4048 + AMP 61314-1 contacts
- 4-pin 20 AWG AMP 171822-4 "Berg" connector for floppies
- 20-pin Molex Mini-fit Jr. motherboard connector
and suggested that most of the PSU's power ought be on 5V and 3.3V rails.
Well, the Pentium 4 came out, and the NetBurst microarchitecture is of course famous for being lavish with heat and power. Now understand that this is all relative. The most power-hungry Pentium III consumed 34.5W, and most of them ate 20 to 25. The 8086 wanted 1.87W. The PC AT came with a 192W power supply for the entire machine, up from the XT's 130W. The hungriest Athlon was, I believe, the 1400MHz T-Bird at 72W. Opterons maxed out at 89W on the 800-series SledgeHammers. Well, the Prescott P4 and its 31 pipeline stages at 3.8GHz had a TDP of 115W, about 25% more than the audacious SledgeHammer 850 (though admittedly the latter was running at about half the clocks).
Well, my AMD Threadripper 3970X has a TDP of 280W, almost 3 times that. You have this story of computers steadily taking less power. Well, they certainly do for the same amount of work. But we give them bigger and bigger problems—Parkinson's Law, "work expands to fill the time available for its completion." And indeed Gustafson's law indirectly formalizes this concept—Amdahl's Law says "the reduction in total time due to increased parallelism is bounded by the intrinsically serial portion of the problem", but Gustafson frames it as "the amount of total work you can accomplish concurrently with the serial portion of the code increases with parallelism." So yeah, a transistor on a 5nm process is smaller and wastes less power than a 90nm transistor, but if you fill the same die area with those 5nm transistors, you're taking way more power, and I'll dig deeply into this later. But a chip of a given area dissipating the same amount of power will have the same average thermal density across all processes. This is known as Dennard scaling.
So yeah your top-tier processors of 2022 are faaaaaar more power-hungry than those of 2004, but we've got tremendously better cooling systems. Until 1989's 486, Intel processors had no cooling. Some 486s got a snap-on heat sink, and OEMs sometimes added 50mm fans. With the Pentium, active cooling was required, and gentlewomen were seen fainting from the vapours when the P54 Pentium Overdrive came with a fan preinstalled, the first of the "stock fans".
By 2005 you started seeing massive heatsinks with 120mm fans and heat pipes. You started seeing high-quality thermal interface material. 2007 saw the first dual tower cooler of which I'm aware, the Thermalright IFX-14 (IFX stood for Inferno Fire eXtinguisher). In 2008 you saw a little Austrian company called Noctua release their NH-U12P, and one year later the legendary NH-D14. I ordered one of the latter for my 2011 Sandy Bridge i7 2600K build, and it was like a piece of alien technology. I'd never seen anything remotely like it.

Anyway back to the ATX motherboard connector. The Pentium IV needed more juice than that available, and it wanted it in the 12 volt form. By this time, processors were running at a little over a volt, much as they do today. Well, more accurately they were running at a wide number of different voltages, all of them less than 3.3V, the lowest voltage available from the PSU (not only do smaller processes allow less voltage, they mandate less voltage, less they die. Put 2V into your modern processor, and you'll kill it immediately). So first motherboards added linear voltage regulators, but those dissipated the volt-amperage product difference as heat. This became rapidly untenable as currents increased, but power MOSFETs that could switch more quickly than bipolar transistors, and which provided synchronous rectification to replace the more resistant flyback diodes, gave rise to efficient and stable onboard buck converters. Your modern N-phase VRMs are simply N synchronous buck converter circuits which pipeline across the switching quantum. This can respond to load changes like a buck converter switching at N times the speed without the increase in switching losses that would be expected. It also allows the heat loss of the switching to be divided across N areas, and can drastically reduce ripple current.
[ DC-to-DC regulator math:
P_D = V_D(1 - D)I_0 P_S_2 = I^2_0R_DSon(1-D) P_SW = VI_0(T_rise + T_fall) / 6T (2T with Miller plate) P_leak = I_leak V P_Dbody = V_F I_0 T_no f_SW P_GDrive = Q_G V_GS f_SW dT_on = DT = D/f dT_off = (1 - D)T = (1 - D)/f D = (V_0 + (V_SWsync + V_L)) / (V_i - V_SW + V_SWsync) ΔI_L_off = integral(t_on...t_on + t_off)(V_L/Ldt = -V/L T_off = (1 - D)T)
So once you have that, you want to work on the highest voltage possible, since more current requires a thicker wire and implies more loss to Joule heating.
[ quantify this ]
So the highest voltage we can get from the PSU is 12V, so that's what the CPU wants. And thus ATXV12 was born, in February 2000, adding a 4-pin Molex Minifit Jr 39-01-2040 carrying an extra 3.3, 5, and 12V pin (plus an extra ground). Now we already had 3x 3.3V pins and 4x 5V pins, so our capacities there rose 33% and 25% respectively. But our 12V capacity doubled, since we only had 1 pin. And given that max amperage is the same across all pins, that's a big increase in total deliverable wattage.
Note that your CPU was now taking a much greater portion of your total power than it was before. So ATX12V 1.0 likewise moved the focus of the PSU off the lower-voltage rails and onto the 12V rails, and ATX12V 2.0 in 2003 made the 12V even more of a focus, due to the recent introduction of power-hungry 12V PCI Express devices (each PCIe slot must be able to supply 75W). You tended to have multiple rails for a given voltage at this time, due to a 240 VA limit per rail up until 2007's ATX12V 2.3. Today, there's not much advantage to a multiple-rail design, and given that balancing your draws across multiple rails can be a major pain in the ass, we can be thankful for that. We're now at ATX12V v2.53, last updated in June 2020.
so anyway, back to testing your power supply. if you don't have a little ATX power tester, you can of course just get a copy of the ATX12V pinout (if you're using EPS, its primary 24-pin connector is electrically compatible with ATX12V) and a paperclip.
[ demonstrate paper clip shorting ]
short the PS_ON pin with any ground, and the PSU's fan ought start spinning. if it doesn't, it's possible that your PSU requires some actual load to turn on the fan, and you might be able to turn this off with a switch. this is applicable to passive power testers like that i just showed, as well—it's not going to require any significant load. if you've got one of the newer ATX12VO 10-pin, 12V-only PSUs, the pinout is different, but you still just need to get PS_ON connected to ground. to get all the information that one of the testers would give you, you'll then need a multimeter; it's pretty simple to test the 4 3.3V lines, the 5 5V lines, and the 2 12V lines. there's also a 5V standby line (supplying power even when the machine is "off"), and the 5V PWR_OK line (driven only when the PSU has stabilized outputs, and they're safe for use), and a -12V line you're unlikely to use unless you've got an RS-232 port.
[ demonstrate testing with multimeter ]
by the way, have you ever wondered why it's 12V, 5V, and 3.3V? i sure have. as best as i can tell, your 12V comes from the automotive world, which makes sense given that 12V is geared towards hard drive and fan motors. lead-acid batteries tend to provide right around 2V per; zinc-carbon and akaline batteries yield just about 1.5V. why is it 2V? let's look at the two reactions going on. at the cathode, we have lead dioxide PbO2 + HSO4 + 3H + 2e -> PbSO4 + 2H2O, water and lead sulfate, with 1.69, nice. that's taking lead in the +4 state to +2. at the anode, we're taking lead from the 0 state to +2, and Pb + HSO4 -> PbSO4 + H + 2e yields -0.356. so this will be driven by the reduction reaction, and we subtract the anode from the cathode to get 2.05. we can then use the Nernst equation for redox reactions to determine the voltage loss as the battery is
[ show nernst equation ]
depleted, as this sulfuric acid is converted to water and both sides become lead sulfate. it's the difference in the strong bonds of water and the weaker bonds of the reactants that lends us our energy. the battery needs a circuit to dissipate because these electrons collect, and inhibit the disassociation of sulfuric acid. wiring batteries in series gives us a voltage equal to the sum of the voltages, so 12V takes 6x 2V or 8x 1.5V batteries. this strikes a good balance between efficiency, which wants higher voltages, and cost/size of battery, which wants lower voltages (if any one of the batteries wired in series faults, the entire larger device faults).
5V is pretty much a straight outgrowth of the chemistry of early bipolar junction transistor-transistor logic, where you needed 2V+ to signal a high, couldn't take 6V without damage due to the chemical composition of your NPN transistors, and higher voltage meant less noise concerns. 5V gave you a high signal easy to reliably hold without crossing into the danger zone. CMOS moved quickly to 3.3V, since voltage is squared in the CMOS power equations (and the smaller CMOS devices allowed you to keep up frequencies with less voltage; less voltage at the same process size will generally lead to lower slew rate (the change in voltage or current), with a direct result of greater propagation delays, meaning longer cycle times, meaning lower frequency). LVTTL was introduced following this change to interoperate with CMOS more easily, but it came out well after CMOS.
alright, so that was a bit of a digression, but back to my story! so i've got my PSU tester out, and there's no love, no flow whatsoever. the electrons are silent, they're insolent. well, shit. i want to see the rest of the build working, so i throw in an old PSU i've got laying around. once again no love. well, shit! i guess we'll toss the old one and RMA the new one. this is out of the ordinary, though, so i go pull a PSU out of my living room server. i put it in the new machine. nothing. ok, well i just saw this working, so either the motherboard is lethal to PSUs, or what, this outlet is bad? alright, let's test the outlet. well, my monitor is plugged into the same pair of outlets, so that argues against the idea, but i really don't want to contemplate a monster-in-my-motherboard so fuck it, let's get down. a standard north american receptacle is the tamper-resistant 15A NEMA 5-15R, where R stands for receptacle; the corresponding plug is the NEMA 5-15P, and these are internationalized as IEC 60906-2. you'll also see 20A 120V, and for large appliances you'll see the 240V NEMA L6-30R, where the L indicates locking.
two quick facts you might not know:
- the plug's ground pin (the one in the middle) is 1/8" longer than the power blades, or at least it ought be. this is so that it makes contact before they do, grounding it before it's live. grab a nearby cable and check it out if you don't believe me.
- secondly, you'll notice that in the majority of configurations, it's the receptacle that has the live wires behind it, for the obvious advantage that you'd otherwise have powered blades extruding out, ready to shock. one place this isn't true is the headers on your motherboard, but they're 5 or max 12V, so unless you're fellating them, you're more likely to stab yourself than even feel it (your dry skin is thousands or tens of thousands of ohms, quite impervious to 12V; your wet tongue is about 7 ohms. go lick a 9V battery and see).
so how do we test a wall outlet? bah, you've known since you were a child—we want to stick pieces of metal into it. of course, we'll keep some serious insulators between the metal and us. break out your trusty multimeter, put it in AC mode measuring volts, and jam those two probes up into the hot and neutral holes. ideally, do this while the outlet is loaded. we ought get 120V, or pretty close to it, within 5% or so. that's your hot-to-neutral. now measure neutral to ground. this ought be very close to 0. now measure hot to ground. this ought be right back at 120, and it ought not be less than hot-to-neutral.

- if neutral-to-ground is large and hot-to-ground is small, hot and neutral have been reversed. many loads, including most electric ones, aren't sensitive to AC polarity, but some appliances are. fix this if appropriate.
- if hot-to-neutral is greater than hot-to-ground, neutral and ground have been reversed. note that you generally have to have some load to see this, and the more load, the greater the difference. fix this, as a dirty ground can fuck you in a great many ways.
- neutral-to-ground ought have some small voltage in the presence of load. if you're measuring 0 volts while the outlet is loaded, your neutral is likely in contact with your ground. if you're measuring more than a few volts, the circuit is likely overloaded.
hot-to-ground ought be the sum of hot-to-neutral and neutral-to-ground.
as a last check you can perform, you can verify that your AC wave is delivering expected peak. you've been measuring in root mean squared; for AC, that's the constant value of the direct current that would produce the same power dissipation in a wholly resistive load, and probably what you want. but electric devices are converting from the peak of the wave. for a perfect sine wave, which is what you want from your AC, the peak of a 120V rms is 168V. how do we test this? AC is 60Hz, but we only want to look at half of a cycle, so think of it as 120Hz. at 120Hz, a cycle is 8.3ms. so if you've got a 1ms peak hold on your multimeter, engage it, and there you go.
alright, so back to my story. i go test the outlet. well, fuck me, it's working perfectly. ASUS has sold me a snow crash motherboard, that kills every PSU with which it comes into contact. who knows; it might already have turned its hungry eye upon me. i don't want to die assembling a cheap machine for my neighbor. i don't want to be killed by a motherboard. well, let's put this PSU back into the living room machine and get its time of death.
it turns on immediately in the living room machine.
ok, so...what? i put the new PSU back into the new machine, and bring it out to the living room. i plug it in. it immediately turns on, singing songs of jubilation with all the Latter Day Saints and the Angel Moroni. my hardware lives! in the nurturing Avalon of the living room, anyway.
[ peace-balance.mkv ]
so...ok, let's bring it back to the office. no love. let's bring the reassembled living room machine in. unplug the monitor, plug that into the living room machine. on it comes. ok, unplug it, plug that cable into new machine. it lives! in the correct room! so i guess i somehow messed up that outlet analysis, huh? i don't understand how, but i'm excited to have everything working. i leave it there, and plug the other cable, the one in the presumed failed outlet, into the monitor, despite knowing it won't work.
the monitor turns on.
i yelp a little, as i do whenever my house is infested with dark sorcery. but this outlet is known bad! it failed to work with two known-working machines! but this outlet is also known good! it succeeded with multimeter tests! 0 equals 1 and we are locked forever in madness.
do you see it yet?
do you see my stupidity?
yeah, it was the motherfucking power cord. it wasn't that i was drawing too much with the computer—that would lead to heat and potentially slagging. i realized that, and went to test it with my multimeter. as i did so, i saw physical damage to the cord, where it had been sliced about halfway through, who knows how. when i extended it to where the monitor was, it was drawn pretty much taut, and everything lined up. when in a big coiled pile of mess, things didn't. i banished it to the land of wind and ghosts, got another cable from my box of treasures, and smoked weed for about four hours because that was some unholy bullshit.
anyway, that was the introduction. now let's get into the meat of this episode.
An origin story
so i like to get to the bottom of questions. power is fundamentally related to energy—in fact, it's just the amount of energy delivered in some unit time. power is watts, and watts are just joules per second, and joules are work, joules are energy. a joule's a Newton-meter, a joule's a Pascal per cubic meter, a watt-second, a coulomb-volt. an amount of energy, applied for some amount of time. between the idea and the reality falls the Shadow, as mr. eliot said. so ultimately from whence our energies?
Frank Wilczek quipped that "Nothing is unstable."
[ thenothing-neverendingstory.mkv ]
If you want to understand why the Big Bang probably doesn't violate the First Law of Thermodynamics, you want to know about supercooled scalar fields (giving rise to inflation via negative pressures and thus gravitational repulsion), slow-roll inflation reheating (where an inflaton-Higgs evolves towards its true minimum, and its potential is converted into matter), and flat zero energy universes (where all energy is exactly offset by "negative" gravitational energy). this is all somewhat speculative, and i find it kinda unsatisfying, so let's just accept the universe as it looked following baryogenesis. we think we pretty much know what's up from that point.
now if you're unfamiliar with the concept of baryogenesis, it's one of the primary mysteries in modern physics. by one mechanism or another, you have a bunch of matter, electroweak symmetry breaks, and you have a hot pho of massive fermions. thing is, all known mechanisms would produce equal numbers of matter and antimatter. either they all annihilate, or you end up with patches of both. but by all indications, the universe does contain matter, so they didn't all annihilate. and we would be able to detect the boundaries where antimatter and matter were meeting in the cosmos. why the imbalance leading to a universe that appears to be free of antimatter? worth thinking about.
it'll behoove us to do a quick recapitulation of fundamental terminology. the money split is between bosons and fermions. bosons have integer quantum spin, fermions don't. another way of saying this is that a boson's total wave function is symmetric. another way of saying this is that in low-temperature, high-density regimes, bosons display Bose-Einstein statistics, and fermions Fermi-Dirac statistics (hence the names). once things get hot or sparse, quantum effects don't come into play anymore, and you can enjoy Maxwell-Boltzmann statistics for everyone. what really counts from our perspective is that bosons don't honor Pauli's Exclusion Principle. they can smush up into the same quantum states. not so for fermions. note that if you are a bound state of an even number of fermions, you're a boson. when we speak of bosons we usually mean the gauge bosons and the Higgs. gauge bosons are force carriers, in that we can model particle interactions as exchanges of virtual gauge bosons. the Higgs is spin 0, a scalar boson. all known gauge bosons are spin 1, vector bosons. the theorized graviton would be a spin 2 tensor boson. the composite bosons are responsible for the Bose-Einstein condensates you've probably heard of, and superfluidity and other low-temperature parlor tricks, but not particularly interesting beyond that.
the fundamental bosons are all their own antiparticles. photons and gravitons are massless, and lack self-interaction, and it's exactly these properties that lead to the infinite reach of gravity and electromagnetism. the weak nuclear force works with two charged W bosons and a neutral Z boson, all three of them massive. the Heisenberg uncertainty relation smearing out the bookkeeping of virtual particles is inversely proportional to the energy involved, and thus the weak interaction is effective only over short ranges, and it's slow even there. we might have to tolerate massive charged bosons popping into existence, but there's no need to let them live their unseemly off-shell lives on the couch. now you might be asking "but niiiiiiiiick, we know the top quark only decays via flavor-changing weak interactions, but its average lifetime is so shooooooooooooort niiiiiiick". well, the top quark approaches 175GeV. it doesn't need to borrow virtual bosons at the First Bank of Heisenberg. if a 172GeV top wants an 80GeV W boson, it whips and drives the little bastard. gluons are mysterious, sublime. i don't pretend to understand their ways. honestly, i don't fuck with gluons at all.
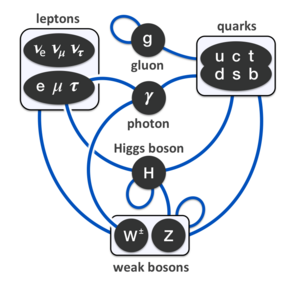
so, the fermions: leptons, quarks, and composites. here's the good stuff. well, not just yet, because first we have to deal with bullshit neutrinos and the even more thoroughly bullshit antineutrinos. actually, neutrinos might be their own antiparticles, who knows, they're worthless either way. if you've heard of the search for "neutrinoless double beta decay", a bunch of very unhappy japanese and italians are trying to figure this out, morlocks in salt mines and giant tanks of ultrapure water, counting scintillations and subtracting expected tritium decays and just generally living their worst lives. there are three distinct neutrinos, all so weak-willed and devoid of identity that they oscillate freely between one another. trillions transpierce you each second, but they might as well not. neutrinos have mass, but they might as well not. i loathe neutrinos.
rounding out the leptons (lepton by the way from the Greek λεπτός for "thin") are three generations of electrons and their antiparticles. the electron, muon, and tau, and here we know they are not their own antiparticles, so we have the positron, antimuon, and antitau. all but the positron and electron are unstable, but the positron and electron are our first truly stable massive particles, though they can annihilate one another yielding photons. electrons are friends. we'll be getting very close momentarily. neutrinos mainly serve to conserve energy and lepton number in decays. a purely leptonic decay always results in a lepton of lesser mass, a the neutrino corresponding to the decaying lepton, and an antineutrino corresponding to the decay product. this latter negates the new lepton number; the former carries away the ghostly memory of the original lepton. the tau can decay via hadrons, but the muon hasn't sufficient mass.
our final pointlike, fundamental particles are of course the quarks, all of them fermions. quarks are the sluts of the standard model, interacting with all four forces, six flavors of hot mess. you don't get quarks by themselves at any reasonable state, but hadrons begin to boil into a quark-gluon soup around the Hageborn temperature: 150MeV (1.7 terakelvin). hadrons (from the Greek ἁδρός for "stout") are bound collections of quarks: mesons (Greek μέσος for "middle") pair a quark with an antiquark having its anticolor, while baryons (Greek βαρύς for "heavy") combine three quarks of different color (color is the tripartite charge of the strong interaction). the unstable mesons are of little interest to us, and we'll not speak of them again outside pion-mediated residual nuclear force. baryons, on the other hand, are quite useful if you're a fan of atoms. the proton and neutron are the lightest and second-lightest, respectively, possible baryons, and thus the stablest. indeed, protons seem completely stable, supersymmetry be damned. so that's the end result of baryogenesis.
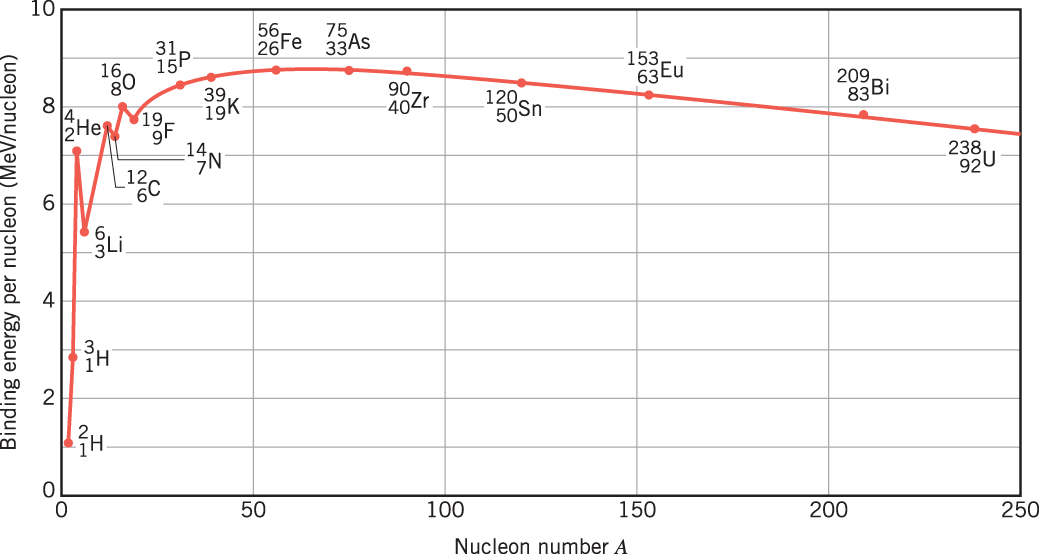
remember e=mc^2. for now, we'll be working in terms of energies and masses. nuclear rearrangements are energetic enough to manifest as a significant fractional mass change. here's the curve of binding energy. as it rises, things are bound more tightly, with less mass per nucleon. as it falls, the binding is less tight, and thus nuclear potential energy is available. it's these nuclear potentials which give rise to everything that follows in the universe. there's no work that can be extracted from the thermal bath of primeval leptons and bosons.
a neutron is made up of one up and two down quarks, with a rest mass of 939.565MeV/c^2. the proton boasts two up and one down quark, for a rest mass of 938.272MeV/c^2. the up is the lightest quark, and doesn't change without good reason (external energy). not so with the neutron, which as you probably know decays to a proton outside the nucleus, with a half-life of about 612s—the beta decay of Fermi. calculating that 612s half-life is pretty non-trivial, and in fact even measuring it is pretty difficult. there are currently two measurements of the average free neutron lifetime, one from "beam"-style experiments and one from "bottle"-style: 878.5±0.8s and 887.7±2.2s. both experiments seem sound. no one yet knows the truth. neutrons can't melt steel beams!
sorry that i can't calculate neutron lifetimes for you, so let me quickly show you how to get average lifetime from half-life. it's a pretty trivial bit of calculus. the probability of decay for a particle follows an exponential, so we expect after time t with N_0 starting elements that about N_t = N_0*e^(λt) remain. λ is the decay constant for the sample. to get the half life, we set N_t equal to N_0/2 (we want half remaining), and set that equal to N_0*e^(λL_H). divide out N_0, take the natural log of both sides, and divide out λ:
[ ln(1/2)/λ = L_H ]
so half-life is ln(2) over λcurve, or about 0.693/λ. similarly, there's a probability of decay of λe^(-λt). we want the probability of not decaying, so integrate this over t and subtract it from 1. the result is e^(-λt). we get the mean value, λ∫te^(-λt)dt. now integrate that fucker by parts, yielding 1/λ. so average lifetime is about 1.443 times the half life.
∞
[ average lifetime = ∫t d/dt (1 - 2^(-t/L_H))dt ]
0
inside most nuclei, it's usually a more energetic state to flip to a proton, due to the Pauli exclusion principle and electrostatic repulsion.
at first, neutrons and protons are freely converting, due to thermal energy well above the 0.78MeV necessary to promote a proton. deuterium is formed but destroyed almost as quickly:
deuterium mass: 1875.6MeV product mass: 1877.05MeV delta: 1.45MeV
and without deuterium, it's pretty much impossible to fuse anything heavier. but as the temperature drops to about a tenth of a MeV, deuterons become stable. most of them will fuse into helium 4 nuclei, aka alpha particles. note that He4 is a pronounced local maximum on the curve of binding energy. we don't get any higher than this, as there are no stable 8-nucleon isotopes, and there's not enough time for rare triple-alpha fusions. on that note, this primeval nucleosynthesis is *not* the same scheme as what goes down in stars: stars require the much slower proton-proton chain, as they burn any deuterium in the first few million years of the protostar period.
so we emerge from big bang nucelosynthesis and recombine into atoms with about 25% helium by mass, .01% deuterium, 74% protium, and a tiny bit of crap. we're definitely not matching this distribution, but the stage is set.
giant clouds of diatomic hydrogen exist in various densities and heats. wherever masses too large or cold to overwhelm their gravitational potential. by the virial theorem, thermal internal energy must exceed half of the gravitational attraction. otherwise, assuming the Jeans criteria are met, gravitational collapse begins in the center of the cloud. Kelvin-Helmholtz contraction and infall of gas raises the temperature to a million K, deuterium-protium fusion begins. at 10 million, at the high compressions and reaction volumes available, proton-proton fusion can begin. Deuterium is easier to fuse because you have two nucleons providing strong force attraction for every one providing electrostatic repulsion (for this same reason, deuterium-tritium fusion is still easier, and that's why D-T fusion is planned for most terrestrial fusion efforts).
let's talk for a second about the mechanics of nuclear transitions. in fusion, we're looking to move up the curve of binding energy by creating larger products. at the temperatures where this can happen, atoms are fully ionized, stripped of electrons—just protons flying around by themselves, each with two ups and one down. an up has a charge of 2/3, a down -1/3, so we have 4/3 - 1/3 = +1, the expected charge on the proton. two protons are going to strongly repulse one another due to the electric charge. in fact, classically there's no way this reaction could proceed at stellar temperatures. with quantum tunnelling in play, however, if we can get these close enough, there's a chance they can link up. the diproton is extremely unstable and disassociates immediately, but if we happen to get a weak interaction at just the right time, one flips to a neutron, and we get a precious deuterium.
in fission, we're going the other way, moving up the curve of binding energy with smaller products. the strong force decays exponentially after a certain, short distance, about the length of four nucleons. the electromagnetic force decays quadratically throughout space. as the nucleus gets larger, electric repulsion begins to approach the attractiveness of the residual strong force. only a small number of nucleons can attract any given nucleon, whereas all protons are repelling one another. at a certain point, addition of a neutron tips the balance: the nucleus deforms into a dumbbell shape, the repulsion takes over, and the nucleus fissions. of course, we've not yet had any supernovae, nor neutron star collisions, so there aren't any heavy atoms to split.
in either case, we need the extremes of the curve to get the largest energies. here, as in everything, nature returns to a gooey, undifferentiated mean. in this case, everything converges to nickel and iron. and as you might thus expect, we see large peaks for both in our prevalence chart.
the solar temperature is generally higher than that of its planetary disk. by the Wien law, we know the energy per gamma is substantially higher; fewer of them are reaching a planet compared to the lower-energy reradiated photons, despite summing to about the same total energy. as this represents fewer macrostates, the entropy is lower. unlike high-entropy waste heat, this is useful. these are the dank photons. these are the wu-tang shit, that shit that gets you high. we can extract work from them.

once we get through to the current third generation of stars, there are lots of metals, rare high-Z elements. from these we get the sweet thorium and uranium we can fission. deep within our own planet are radioactive isotopes, mostly potassium and actinides, providing radiogenic heat. together with Kelvin-Helmholtz contraction and internal frictions, and of course insolation, this represents earth's energy inputs. all of them. that's it. if this is more energy than earth radiates, we heat up. if this is less energy than earth radiates, we cool down. calories in, calories out, or photons anyway.
so every source of power we might use—fossil fuels, geothermal, piezoelectric solar, wind, beast, falling water, biomass, solar, hydrogen fuel cells, tidal, cows with tubes shoved up their asses so we might milk their heavy farts for methane, methane we'll burn to power the grills in which we'll cook them, frenetic dancing, magnifying glasses with which to incinerate ants, yes even the power of love—originates in these few nuclear, gravitational, and frictional sources.
Computer's gotta eat
so why does our computer need power? alright, sure, we need mechanical power for motors. and there's lights, they take power, we all understand that (fun fact: America's on 120V largely because Edison's carbon filament light bulbs ran on 110V, and it would be expensive to rip all our electric infrastructure out. europe had the gift of world war ii to handle that for them, and they came back at the more efficient—but less safe—240V). need power for our rgb fans and rgb keyboards and rgb dinner guests etc. but i don't see anything going on in my CPU—what's it doing with 280W?
[ pricecan.mkv ]
you're surely aware that the cpu is built up of transistors. my amd 3970x has 15.2 gigatransistors on TSMC's 7nm process. nvidia's a100 has 54 billion. graphcore's colossus MK2 boasts 59.6 billion. samsung built a 1TB eUFS VNAND flash with 2 teratransistors. but the reigning dance hall champion, at least in the open literature, is the Wafer Scale Engine 2 from cerebras systems, packing 850,000 cores, 2.6 teratransistors, and 40 gigabytes of SRAM in a die not much larger than my junk. it's impossible to say how small a transistor-like system can be, but we are pretty sure that we know the minimal cost of a unit of irreversible computation (if you've never heard of reversible computation, go read Feynman's Lectures on Computing, right now, but it's basically computing using exclusively bijective functions). you've got Boltzmann's entropy formula
[ S = k_B lnW ] for W states in a system
entropy is defined here as E / T, so multiply both sides by T, and substitute 2 for W:
[ E = k_B T ln2 ]
and that's Landauer's principle, and you really ought go read john arcibald wheeler's "it from bit", which is fantastic.
k_B is the boltzmann constant 1.38 * 10^-23 J/K. so at 30C, we've got 303.15K, so 2.90 zJ. we're many orders of magnitude less efficient than this, so hey cmpe pukes, maybe get off your asses and do some zeptoscale work. note that in open space, we've got just 2.7K. that's a mere 25.8 yoctojoules.
[ willie.mkv ]
still, that's only two orders of magnitude down—we're not at all asymptotically approaching zero or anything. infinite additional cost to cool would be rewarded with negligible reductions in cost to compute.
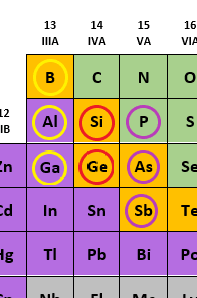
anyway, how does a transistor work? a transistor, in any of its many dozens of implementations, is fundamentally a semiconductor device. what's a semiconductor? a semiconductor lies between conductors and insulators, and more importantly, its conductivity at a given moment can be controlled by a current or temperature (unlike a conductor, which becomes less conductive with heat, a semiconductor becomes more conductive with heat). semiconductors are well-represented by the Group 14 elements, as several are metalloids, and have 4 valence electrons and tetravalent crystals. carbon is an insulator because it holds its electrons too tightly—its 4 valence electrons are all in the second shell (this is unfortunate, since isotropically pure diamond is the best thermal conductor, about 5 times more conductive than copper at room temperature). silicon's valence electrons are in the easygoing M shell, and germanium's whip around in the N shell's 4s and 4p. once we get to tin and lead, we're definite metals, and our 5- and 6-deep shells quite good conductors (the lead valence story is kind of ratchet, due to relativistic effects arising from its heavy nucleus and the innate funkiness of the f subshell: remember, by orbital energies instead of shells, the Pb configuration is not 4f¹⁴5d¹⁰6s²6p², but 6s²4f¹⁴5d¹⁰6p². those 6s are held quite tightly, and the 4f/5d are all over the place. this raises the energy of formation of PbO₂ while lowering the energy of formation of PbSO₄, and that's great for a reaction of Pb+PbO₂+H₂SO₄ -> 2PbSO₄ + 2H₂O! without this relativistic effect, the voltage on a lead-acid battery would be about .4V rather than 2.1V, and your car wouldn't start. this is, incidentally, why tin-acid batteries don't work, whereas they might be expected to be from a non-relativistic chemical analysis).
so, back to semiconductors. they're not really good for coaxing into either insulation or conductance on their own, even with current applied, but by doping them with trivalent Group 13 or pentavalent Group 15 impurities (at very low, regular rates, like 1 per 100 million or so), we can bring them closer to the sides of the graph, to where a small current can take them over the threshold. and that's the really key part of transistors: they allow a small current to control a potentially larger current. they're thus natural amplifiers, among other things. basically you've got three signals carried on wires. for the MOSFET, we call these source, drain, and gate; for bipolar junction transistors, we call them emitter, collector, and base. we can use the gate to control whether current flows from source to drain. the voltage can be negative or positive depending on the doping we performed during cultivation of our boule, but it's important to know that MOSFETs only actively consume power when switching (unlike BJTs, which are always consuming power).
-=+ FIXME need to explain n-type vs p-type +=-
now, as promised, the CMOS power equations, where you can see why i claimed power to be quadratic on supply voltage:
[ P = Pstatic + Pdynamic + Pshort-circuit P_static = V * I_leak P_dynamic = α * C * V_supp² * F P_short-circuit = V_DD * ∫t_0t_1 I_SC * τ dτ
But, since we can reduce Pshort-circuit towards 0 by scaling down supply voltage with regards to threshold voltage (VDD ≤ |Vtp| + Vtn → Psc = 0),
P = Pstatic + Pdynamic ∎ ]
so to answer our original question, we need power—electric power, zee Watts delivered as polarized direct current—to drive all those transistors. we need power to make the bits flip! that's dynamic power. there's also static power, a function of voltage and "leakage current". so voltage contributes to both static and dynamic power consumption, linearly in the former case, quadratically in the latter case. we want badly to bring voltage down! unfortunately, simply reducing supply voltage makes us switch more slowly (which can result in more dynamic power consumption, since α might go up). it also reduces our noise margins. ok, well let's reduce our threshold voltage in concert, no biggie. unfortunately, this increases leakage current, and at some point the losses due to leakage current can exceed the actual useful power. this is why your CPU is still around 1 to 1.2V, rather than half a volt or something. leakage current sucks ass, and is a big part of why we've been hearing about the end of Moore's Law all this past decade.
now if you're just a braindamaged cs major and have never seen gates expressed in transistors, it's probably worth doing so. let's build a 2-input NAND gate, which is of course along with NOR a universal boolean gate.
actually, it occurs to me that some of you might not be aware of the completeness of NAND and NOR logic. so first off, know that processors are not being designed in terms of logic gates, so this is kinda immaterial. but, since it's a pretty cool construction:
we need functional completeness, i.e. the ability to generate every possible truth table. there are four unary functions, sixteen binary functions, 256 ternary functions, etc., 2^2^N for n arguments.
[ binary hasse diagram ]
unary functions: pass, negate, const 0, const 1
so remember, NOR is NOT of OR.
[ nor image ]
so to negate in NOR, double up the input. 0 OR 0 is 0; 1 OR 1 is 1. negate gives us pass: use two NORs. double the input, and double the first output. const 0 in NOR is just 1 NOR A. const 1 is const 0 with a NOT.
negate in NAND by pairing the input with 1. 0 AND 1 is 0; 1 AND 1 is 1. const 0 is 1 NAND A. const 1 is const 0 with a NOT. good times.
using similar strategies, we can build up whatever, and we can prove this using connectives and clones, as demonstrated in Post's lattice.
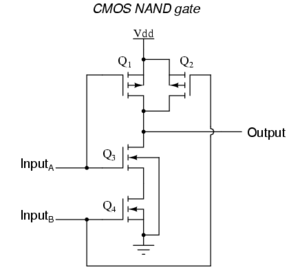
so we can build this with two MOSFETs per input. if both A and B are low, both pmos are on, and both nmos are off. the output gets V_DD due to the on pmosen, and the off nmosen prevent out from discharging to ground. so this is high. if either A or B (but not both) is low, V_DD passes the parallel pmosen, and cannot reach ground due to the serial nmosen. when both A and B are high, both pmosen are off, and there is no path from V_DD to the output. both nmosen are on, meanwhile, discharging the output line. and thus this case, and this case alone, goes low, which is exactly what we want for NAND—we're true whenever not (a and b).
NOR is left as an exercise for the reader. it isn't hard.
[ ∞
E_C = ∫ i_VDD(t)v_out dt
0
= C_L / 2 V^2_DD ]
we like electricity for this because it can be quickly and flexibly controlled. it's totally possible to build a transistor without semiconductors. hell, we can build one without electricity. let's say we hire a bunch of gender studies phds and give them all heated blankets. the blankets can be controlled at 1C levels via a control, and each participant has a control, which they believe to be attached to their own blanket. the blankets can range from 20 to 40C. assume the participants' ideal temperature is 30C, which just happens to be the ambient temperature. we can examine the participants' controls relative to their actual temperatures. if the control is below the actual temp, it is a 0. if the control is above the actual temp, it is a 1.
pick up the control for a blanket, and set it to 40. when the blanket reaches 30C, the participant will begin requesting it to cool down (output 0). this will continue until we reduce the temperature. likewise, set it to 20. when the blanket drops to 30C, the participant will begin requesting it to warm up (output 1). treat their requested control as an output line, and our effected control as an input line, and we've just built an inverter. this logic gate's maximum switching time is equal to the time necessary to raise or drop the temperature 11 degrees.
but hold on, we can make these people even more useful. map input 1 to 30, and input 0 to 40. if the output wants a change, that's a 1; if no change is desired, that's a 0. now give a participant two blankets sewn together to appear as one. hook your inputs up to the two controls. well we've just built a NAND gate. given a sufficiently large cohort, we could build a computer.
[ matrix.mkv ]
but that all sounds like a bit of a pain in the ass just to do some matrix multiplications. not too fast, either. certainly not ready for the 4k realtime raytracing. so electricity affords us the tiny powers and fast switching necessary to do serious computing.
alright, we get it, we want some electricity for this machine. but why do we need to go to the wall outlet for it? whatever happened to self-sufficiency and pulling oneself up by one's bootstraps and such?
well, first off, what is electricity really? when we say we're supplying 120 volts at up to 20 amps, what does that mean? supplying power means we're delivering watts; we integrate watts over time to get work in joules, so watts are joules per second, and thus newton-meters per second. everything electricity flows through has some non-negative resistance. if that resistance is 0, the conductor is a superconductor (which by the way does *not* violate the Second Law of Thermodynamics, because it's not doing any actual work). anywhere you're deliberately converting electric power to some other kind of energy shows up as resistance. we can relate watts to ohms in a conductor:
[ W = Ω * I^2 W = Ω / V^2 W = I * V ]
from these definitions we'll take two powerful laws. the first is ohm's law for ohmic materials, basically defined as "materials for which ohm's law applies":
[ I = V / R ]
note that as voltage goes up for a given resistance, current goes up as well, perhaps contrary to what you'd expect. for a given wattage, as voltage goes up, current goes down, but wattage is inversely proportional to resistance. and that makes sense, right? more resistance means less current to flow, meaning less power. in an open circuit, the conductor is air, a powerful insulator, and negligible current flows for low voltages.
a watt is an ampere flowing across a potential difference of one volt; it's one volt-amp. ok so what's that? well fundamentally we have some material, a conductor, and it's made up of atoms which have some loosely bound electrons. these are usually metals, because their valence shells are far from full. it's got a cross-section, and the number of electrons is proportional to that cross section. in order to make current flow, we need to create a voltage difference across a path. this is accomplished at your outlet by having two wires, a hot and a neutral. in a battery, we have two terminals of opposite polarity. when you plug a conductor in, a path is made, and now electrons can shuffle along. nuclei don't move, but the valence electrons do, each representing one fundamental charge. an amp is about 6.24 elementary charges. to conduct more amps, you need a bigger conductor; the number of charges that can move is directly proportional to the cross-section of the wire, and thus resistance drops. joule's first law tells us:
[ P = I^2 * Ω ]
as a wire grows longer, however, resistance goes up. so the heat a wire dissipates is entirely a function of the amperage, the geometry of the wire, and the material's resistivity, which is a function of temperature. Pouillet's law gives us:
[ R = rho * length / area ]
as heat goes up, so does resistance, in what can be a positive feedback loop. positive feedback loops are Bad Shit, to be Avoided. here, they take the form of your wire's insulator catching fire.
if you happen to know the magnitude E of the electric field and the magnitude J of the current density at a point, you can solve for rho at that point:
[ rho = E / J ]
and we can use that to derive Pouillet's law when E and J are constant:
[ rho = E / J, E = V / l, J = I / A, rho = V A / I l, rho = R * area / length ]
at 25C, AWG 20 is 10.4 ohms per 1000 feet, but at 65C that number is 11.9, a full 10% more. this dissipation is of course reflected as voltage drop, with more drop as the wire gets longer.
for a wire of 5m or so, we're safe pulling 20 amps through 12AWG, 15 through 14 AWG, 10 through 18AWG, and 7 through 20AWG. at 120V, it's unlikely that you need more than 16AWG up until a 1600W power supply. most 1600W PSUs are 80 Plus Platinum or higher. at 89% efficiency, a 1600W PSU is pulling just about 1800W from the wall, or just below 15 amps. this is why you don't tend to see consumer PSUs above 1600W—common breakers in North America are rated for 15 amps.
note that voltage does not affect joule heating! these cords tend to be rated for 300 or 600 volts. all insulators, including air, have a dielectric strength, beyond which they break down, leading to voltage arcs.
but what's a current density? current density is the amount of charge per time flowing through a cross section, amperes per square meter, and it's dependent on the charge-carrier number density, the charge on the charge-carrier, and the drift velocity. working with electrons, our charge is -1.6e-19 coulumbs. drift velocity is the net average velocity of the charge-carriers. electrons are bouncing around schizzily at high speeds. we can calculate these speeds; electrons in a metal are basically a fermi gas, and the fermi velocity then is the fermi momentum over the fermion mass:
[ v_f = p_f / m_0 ]
where said momentum is:
[ p_f = sqrt(2 * m_0 * E_f) ]
the fermi energy is:
[ E_f = hbar^2 / 2m_0 * (3pi^2 N / V)^(2/3) ]
copper has one free electron, a density of 8.96 g/cm^3, and an atomic weight of 63.5 g/mole. plug through Avogadro's number, and we get a free electron density of 8.5 * 10^28 per cubic meter. that yields a Fermi energy of 7 eV. that's 11.2 * 10^19 J, and since these are non-relativistic, we can then take our friendly old e = m/2 * v^2 from kinematics, set:
[ v = sqrt(2E_F / M_0) ]
and get a Fermi velocity of 1.6 * 10^6 m/s. so they're all over the place, about 1 and a half megameters per second. that's still only about 1/300th of the speed of light.
the drift velocity is much, much more sedate. drift velocity is:
[ u = mσV / ρefℓ ]
where m is the molecular mass, rho is the density, and sigma is the conductivity, which is just the inverse of resistivity. for macroscopic wires, though, we have the much simpler
[ u = I / nAQ ]
we have n from earlier, 8.5*10^28. let's say our wire is 2mm in diameter, so it's a 1mm radius, so multiply that by pi and then by 1.6*10^-19, the charge on an electron. let's say we've got 1 A flowing. in that case our drift velocity is 1 over 42780, or about 2.3*10^-5. that's eleven orders of magnitude slower than the fermi velocity. they're crawling along at about 2 hundredths of a millimeter per second. sad! multiply that by the charge density, and you get the current density. and with that, you can calculate resistance at a point.
now, if the electrons have a barely perceptible net velocity, how the hell does a light turn on effectively as soon as we flick the switch, closing the loop? well, electrons are carriers of the charge, but they're not the charge itself. the charge is propagated along as a change to the electric field, exploding forward far more quickly than the electrons themselves (indeed, faster than any massive particle will move without tremendous energy input, as we know from special relativity). a final speed we want to look at is thus the signal propagation velocity, the speed with which this change to the field ripples out. btw, you've probably heard the photon described as the force carrier of the electromagnetic force; please do not try to interpret this in terms of photons. down that path lies madness. Deriving the signal velocity from first principles gets deeper into classical emag than we really want—if you're interested, look at the Drude model and damped oscillators and traverse waves, and Godspeed. we'll instead accept
[ v_s = c / sqrt(e_r u_r) ]
where e_r is the relative permittivity, and u_r is the relative permeability. for copper, we get a result that's about 2/3 the speed of light. not so relevant for our bedroom lighting, but quite relevant when designing at the nanometer scale.
so what's the upshot of all this? we can't put too many volts into a device, or we'll kill it, based on fixed properties and geometry of the device. we can't put too few volts in, or it won't operate properly, where that might also mean damage to the device. we can't put too many amps through a wire, or we'll set the wire on fire. the more voltage we deliver, the fewer amps for the same wattage, and thus the less waste. work wants a certain number of watts, performed at a certain voltage; it presents a resistance in ohms, which determines the number of amps. the charge selects the number of amps, and you must ensure its intended voltage matches the provided voltage, and that your wires are safe for the amps.
so now that we know what electricity is, can we not dispense with the electric company? let's say we wanted to power the computer using our biological energy. or, you know, maybe someone else's biological energy. holy shit, did you know that british prisons would have treadmills the prisoners walked? check it out, you were in a little concave box so you couldn't see anything, and you had to walk, and they ground wheat or sometimes nothing, in what was called "grinding the wind." alternatively there were "crank machines" where you had to do a certain number of rpms. fucking ghastly shit. and certainly going back through the Corrective Labor Colonies of the Soviet Union's GULAG, the Zwangsarbeiter of Operation Todt, the chattel slavery of my own Southern United States, the diamond mines of Sierra Leone and Africans enslaving Africans pretty much since there were Africans, to Hammurabi's Code and probably the first homo sapiens to domesticate, there's a long and grim history of putting other people's biological energy to use. and for a long time, that was really the only way to scale energy available to most endeavors.
so! imagine you're the Fresh Prince of Dubai, and you're thinking hrmmm, conflict diamonds are tough cheese these days, what ought i have my slaves mine? and then it hits you, ahh, i'll have them mine bitcoin! but now you have a quandary: what's the better bottom line for your petrodollar: have them ride bikes to power ASICs, or simply use them as fuel for a roaring furnace? well, first off, burning human corpses is not an energy-efficient proposition, because we're mostly water. if you're a 200-pound fatty composed 65% of water by weight, that's about 60kg of water. assuming you need raise that 60L by 70 degrees celsius, and then vaporize it, you're talking 2550J per gram, or about 150MJ. A megajoule is comparable to a car going 100mph. when we burn dinosaurs, we're catalyzed by 500 million years of catagenesis.
well it's pretty easy to guess. one horsepower is 746 watts. we've got a psu that consumes about a kilowatt, so just about one and one third horsepower. can you pedal with the power of even one horse? i cannot. but let's do this rigorously, or at least in a way that doesn't involve standard metric horses. that'll require going back to our high school biology.
What is life?
what is life? well, physicist schrodinger tried to answer that in 1944 (he was in ireland at the time), and he said it's highly ordered low entropy arrangements which evade the decay to thermodynamic equilibrium mandated by the Second Law of Thermodynamics by homeostatically maintaining negative entropy. that requires an input of free energy, which we'll talk about later. now cells can't store significant amounts of free energy. it would raise the temperature, and that denatures proteins. most enzymatic proteins base their tertiary structure on hydrogen and van der waals bonds, and we're talking weak hydrogen bonds here a few kilojoules per mole. well, a square meter receives about 1.4 kilojoules every second in full sunlight. a nutritional calorie is 4 kilojoules. and that's per mole. divide it by avogadro's number, and you're talking tens of zeptojoules. that's less than an electrovolt. that's not much more than the Landauer limit we talked about earlier, the least theoretical energy required to flip a bit. it's like if every time you added two numbers your brain melted from the effort.
but cells need to expend energy; anabolic metabolism is the building and maintenance of highly-ordered and energy-rich structures from smaller ones. there's a beautiful molecule for this, adenosine triphosphate, and it's ubiquitous in biota. cell nucleus? not even all human red blood cells have a nucleus. flexible cells? nah, those are just animals. life has gotten by just fine without cellular differentiation. but as far as we're aware, everything alive has at least one cell, and everything alive has DNA, and everything alive uses ATP as its primary energy exchange, for purposes including DNA synthesis. why? well, it can be hydrolyzed, which is important since cells are mostly water. it can be built up by multiple routes, both aerobic and anaerobic, from catabolic results. hydrolysis releases some dozens of zeptojoules as energy of the resulting gamma phosphate, and remember, that's about what we need to change protein conformations.
for instance, the sodium-potassium pump is critical to maintain cellular electropotentials. it's common to all cellular life, and thus all known life. the pump pushes sodium ions out of the cell, where they normally accrete, and pulls potassium in. this is catalyzed by the phosphorylation of membrane transport proteins. normally the protein weakly binds 3 sodium ions. upon phosphorylation, it undergoes a conformal change, releasing the sodium outside the cellular membrane. in this higher-energy conformation, it weakly binds two potassium ions. this kicks out the phosphate, restoring the original folds. free energies in these processes depend on concentration gradients and pHs and such, but some reasonable values would be 95 zeptojoules in hydrolysis vs 71 for the active transport. this represents a 75% efficiency in ATP use, which was oxidatively phosphorylized at about 40% efficiency in the mitochondria.
let's do a basic check on this. the average male is known to radiate about 100W of heat when resting. our metabolic rate is equal to heat exchange with the environment plus external work we're doing. we're not doing external work, so it's all heat exchange. 100W over a day's 86400 seconds is 8.64e7 joules, which is about 8640 kilojoules, which is about 2057 calories. and that's pretty close to the recommended daily intake. so that checks out.
it's hard to use that waste heat, because it's (a) hard to capture all of it and (b) it's not reliably different from the external temperature—we don't have a good gradient for heat to flow across. so what about mechanical work? ATP is used to transport calcium ions and deactivate actin. with about 5 millimoles of ATP per kilogram of wet tissue, and about 20kg of muscle in the body, at the 51 kilojoules per mole we referenced earlier, that's 5 kilojoules available for immediate use (about a half-second of maximum effort). there's about 4 times as many moles per kilogram of creatine phosphate, which can rapidly recharge ATP. altogether, there's a best case 40 kilojoules usable within about 5 seconds, so we're talking maybe 8kW during that time. ATP is further energized by anaerobic glycolysis, limited by lactate buildup after a few minutes of multi-kilowatt metabolism. beyond that, we're stuck with aerobic respiration, and with conditioning we can get out a few hundred watts of metabolism. this is requiring a great deal of oxidation and heat transport to maintain. using our largest muscles, the glutes and quads, we can hit about 20% efficiency with cycling. electric conversion then runs at maybe 60% efficiency, twelve percent of that outflow. so we're talking a few dozen electrical watts sustainable by a well-conditioned person. good for charging your phone, not so great for running our computer.

we don't have enough time to go deeper into the body's thermodynamics and energy budget, but it's fascinating. as one last note, if you've ever wondered why carbs and proteins are considered 4kcals a gram, and fats are 9 kcals, know that it's the Atwater system, it's disgestibility-scaled (proteins have more raw energy, but we piss away 20% of the protein we take in), and fats lack oxygen, supplying only energy-rich CH bonds (oxygen being the "drate" in "carbohydrate") per gram. of course, everyone knows the real key to nutrition is DRAINO-brand clogbuster. Drink it, put it in your eggs, or just rub it on your gums: you can't go wrong.

so if we had enough people or yaks or whatever devoted to it, sure, we could power our computer. of course, we'd need to feed them, and simply burning that food would be far more efficient than going through the repeated reductions and oxidations of human metabolism (among other reasons, this is why The Matrix was full of shit and stupid). the waste products are about the same: carbon dioxide and water. indeed, when you're losing weight, and you think "hrmmm where did my ass go?", it went almost entirely into carbon dioxide, water, work, and heat—it was burned, just without combustion.
alright, but i live in a high rise, up on the 32nd floor. now even if i had the food resources, it's hardly a place for power-generating yaks. there are furthermore several hundred other units here, and any attempt to bring in the corresponding yak volume would draw some very low-pH words from the HoA. there'd be a great deal of yak shit needing removal, and that work simply doesn't appeal to the young urban professionals that dominate my building. so we'd like our fleet of yaks somewhere else. likewise, despotic regulation prohibits even controlled nuclear fission within the city core. there is a notable absence of major waterfalls in midtown atlanta. so however we want to generate energy, we're going to need to transport it. though do note that sufficiently dense sources of energy generation and efficient storage can eliminate this need, and of course there's very active work in distributed solar generation and microgrid batteries.
Move 'em out
now we can transport any kind of energy. mechanical energy? sure. an internal combustion engine oxidizes fuels containing chemical energy to produce pressure, turning a crankshaft, down through the drive train and finally spinning wheels. sound is transported through a medium via the potential of longitudinal and traverse waves, and the kinetic energy of displaced particles. pneumatics, hydraulics, telodynamics, gears, these all exist. london moved 7000 housepower over 180 miles of pipes carrying water at 800PSI. rather than electric lines from Georgia Power, we could have Municipal Belts and Yaks, and somewhere in Georgia's blighted south there'd be tens of thousands of yaks driving a huge belt, and it would come screaming across the sky and power an elaborate system of smaller belts, and there'd be a belt going to your house. you'd of course have to constantly yell over the mindnumbing cacophony of thousands of belts, and you'd have little kids getting their faces sanded off, and sometimes the belts would snap with tremendous force, taking out whole neighborhoods, but Robert Moses might have dug it.
so when you look at the efficiency of generation, and of transport, and especially the ease with which it can be applied to different tasks, centralized generation of electricity transmitted via metallic conductor is the only way you can generally drive the modern world (decentralized generation isn't as efficient, but it's generally using renewable primary energies, and it tends towards very low OpEx. unfortunately, you have problems like the geographic restrictions of solar). so we've developed ways to cost-effectively and safely convert just about every form of primary energy into secondary electric power. we haven't yet locked down net-productive fusion, and we're of course drastically altering our atmospheric composition through combustion and deforestation. remember earlier, we said that if photon energy out was exceeded by photon energy in, the earth heats up. well, greenhouse gases prevent photons from leaving by absorbing and reradiating them.
[ spectrogram of absorption by atmosphere ]
indeed, were it not for existing greenhouse gases, the earth's surface would probably run about -18C. but whatever we end up doing for primary energies, the result will still be electricity. the United States generates a little over 4 trillion kWh at utility scale, an average of 130 gigawatts with a maximum capacity of about 1.1 terawatts. a little less than 10% of this is consumed in utility distribution, for over 90% efficiency to the customer. citizens of the first world consume between ten and fifteen thousand kWh from this network per year. should our machine draw a constant kilowatt, that's 6360 kWh right there. that's $318 from Georgia Power at a nickel per kilowatt hour. who knows how much it would be from Municipal Yak.
now electricity is not generally available from nature. bioelectrogenesis finds its place in microbial fuel cells. geomagnetism? satellites can use electrodynamic tethers to harvest energy from terrestrial magnetohydrodynamics, but it doesn't help us here on the surface. neurons and other minor electrophysiologies work on millivolts and nanoamps. lightning is still pretty useless beyond starting fires. our 4 quadrillion watt-hours require serious industrial generation, and about 80% of it comes from turbogenerators, most of them steam-powered. ahh, the turbogenerator.
[ powertriangle.png ]
large ones hit about 2GW of output, though this will be typically reported in MVA. wherever you see VA, which you might want to call "watts", you're seeing apparent power, the power both dissipated and returned. if you see VAr, that's volt-amps-reactive, and it's the reactive power—power returned in the load. watts are reserved for the true power, the power dissipated by the load. you don't just add true and reactive powers to get apparent power; the three form what's called the "power triangle", with apparent power as the hypotenuse. the angle formed is the impedance phase angle (impedance is a complex number,
[ complex-impedance.png ]
and this gives us the polar form). r represents the ratio of the voltage difference to the current amplitude, and theta is the phase difference between voltage and current. in cartesian form, impedence is R + iX, where R is resistance and X is reactance, the opposition presented to current by inductance and capacitance. by the way, you'll see double-Es and cmpes write the square root of negative one as 'j' instead of 'i', and this is why they pronounce the word "jimaginary", but i was a MATH major by god, and
[ quote-descartes.png ]
Descartes called them "imaginaires" in 1637, not "jimaginaires", and Euler called them i, and Ampère maybe ought have used a different symbol for "intensité du courant" two-fucking-hundred years later. why wasn't it
[ quote-ampere.png ]
"jintensité"? my wife and i used to fight about this. now she's my ex-wife. blame the french.
as frequency increases, inductive reactance increases, and capacitive reactance decreases. an ideal resistor has zero reactance; ideal inductors and capacitors have zero resistance. let's talk about these for a minute. inductance is the ratio of induced voltage to the rate of change of current doing the inducing. let's see how this works. first you have Lenz's law from 1834. in 1831, faraday wraps two wires around opposite sides of an iron ring. remember we said there's not much electricity in nature, that we can harness anyway, but there thankfully *is* ferromagnetism. on the first wire he has a battery, one of the newfangled "voltaic piles". on the other wire, a galvanometer (current detector). well, the galvanometer pings, but only when the battery is connected or disconnected. if the circuit is left open or closed, there's no detected current. also, the ping has opposite signs depending on whether the battery is being hooked up or disconnected.
well, what's happening here? well we have electrons bouncing around like idiots as always. they've got quantum spin and orbital motion.
when he does so, a galvanometer connected to the latter detects a current.he observes that a galvanometer lights up a changing magnetic field this is governed by faraday's law of induction, one of maxwell's four laws:
[ ∮_∂Σ E*dℓ = -d/dt∬_E B*dS, ∇ x E = -∂B/∂t ]
the latter differential form is the Maxwell-Faraday version,